La funzione Totiente di Eulero.
Oggi vediamo una semplice implementazione della funzione Totiente di Eulero che ci permetterà di calcolare tutti i valori della funzione fino ad un certo fissato numero N.
L'algoritmo ha bisogno innanzitutto di un vettore per salvare i dati e di una variabile che ne contenga la lunghezza, nel nostro caso
long N = 10000; int[] phis = new int[N];
L'idea dell'algoritmo è molto semplice: scorrere all'interno di un ciclo for tutti gli interi da 2 a N e cercarne il più piccolo divisore diverso da 1 ovviamente. Dato un numero M cerchiamo il più piccolo numero p (che sarà primo per forza di cose) che lo divide e scriviamo M come il seguente prodotto
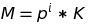
In questo modo dalle proprietà della funzione phi di Eulero (wikipedia per i dettagli) sappiamo che possiamo moltiplicare i valori delle funzioni
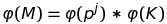
e che
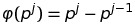
Per fare questa operazione utilizziamo il seguente metodo che restituirà in t il valore p^j mentre restituirà il p il valore del divisore più piccolo.
private static void DammiMinimoDivisore(int i,ref int p, ref int t) { if (2 < i && i % 2 == 0) p = 2; else { var maxcheck = Math.Sqrt(i); for (int k = 3; k <= maxcheck; k=k+2) { if (i % k == 0) p = k; } } if (p == 1) return; while (i % (p*t) == 0) { t = p * t; } }
Come si può vedere dal codice, l'unica operazione matematica non elementare è la radice quadrata. Scritto questo metodo il grosso è fatto perché controllando il valore p o t di ritorno del metodo sapremo se il numero che stiamo indagando è primo oppure no. Nel caso sia primo sappiamo calcolare direttamente la phi (dettagli sempre su wikipedia) altrimenti utilizzeremo i valori precedentemente calcolati per calcolare il nuovo.
Abbiamo raccolto il tutto in una piccola console application
static void Main(string[] args) { long size = 10000; int[] phis = new int[size]; phis[1] = 1; for (int i = 2; i < size; i++) { int p = 1; int j = 1; DammiMinimoDivisore(i, ref p, ref j); if (p != 1) { phis[i] = (j - j / p) * phis[i / j]; } else { phis[i] = i - 1; } } }
Con alcuni piccoli accorgimenti è possibile rendere più efficiente l'algoritmo ma rimandiamo queste modifiche ad un'altra volta. Buon divertimento!
comments powered by Disqus